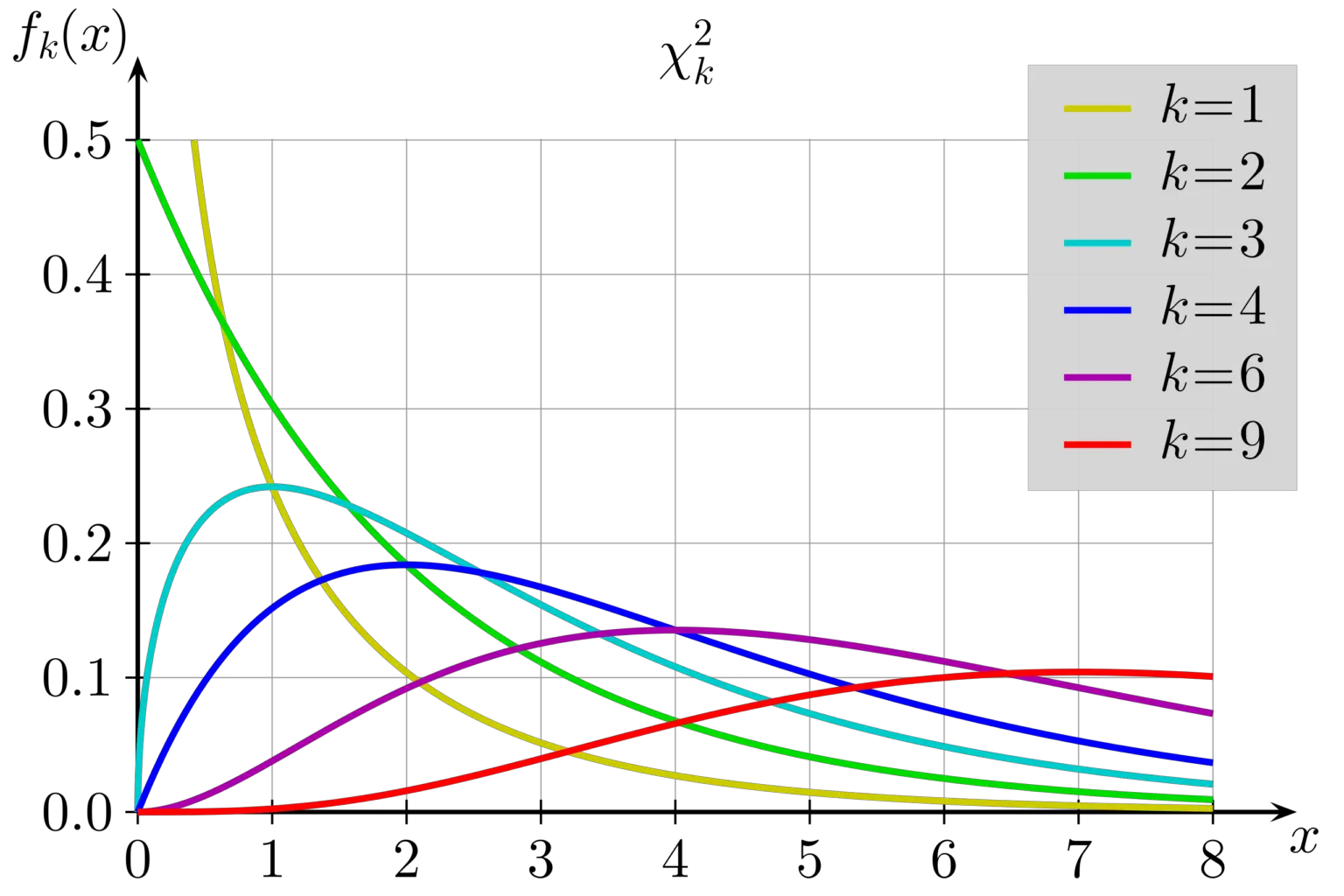
Normal table score distribution read math probability scores probabilities statistics calculate standard values sheet mean compute reorder point find critical
Table of Contents
Table of Contents
Are you struggling with understanding Z Score Chart Normal Distribution? Do you want to know how to use it to your advantage? Keep reading to find out!
The Pain Points
For many people, Z Score Chart Normal Distribution can be a confusing and intimidating concept. It involves complex statistical calculations and terminology that can make it challenging to grasp. Additionally, understanding how to use this tool effectively can be the key to success in various fields, including finance, scientific research, and more.
The Target of Z Score Chart Normal Distribution
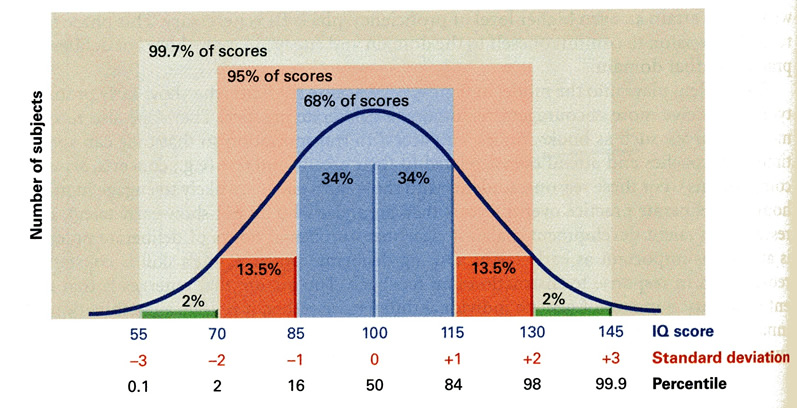
Z Score Chart Normal Distribution is a statistical tool used to determine the probability of a value happening within a normal distribution. It measures how many standard deviations a value is from the mean and allows you to compare values from different datasets. Its primary target is to help you make informed decisions based on the data available.
Main Points Related to Z Score Chart Normal Distribution
By understanding Z Score Chart Normal Distribution and related keywords such as standard deviation and normal distribution, you can make better decisions and gain insights from your data. This tool is especially useful in finance, quality control, marketing, and other fields where decision making based on data analysis is crucial. By knowing your Z scores, you can determine the probability of a value occurring and make informed decisions.
Z Score Chart Normal Distribution Explained
When I was working as a financial analyst, I was tasked with analyzing investment portfolios to determine their risk and return potential. Using Z Score Chart Normal Distribution, I was able to determine the probability of a particular portfolio’s return compared to the broader market. This allowed me to make informed decisions regarding which portfolios to invest in and which to avoid.
Z Score Chart Normal Distribution works by calculating the number of standard deviations a value is from the mean. The further away a value is, the less likely it is to occur. It’s essential to understand that a Z score of 0 means the value is equal to the mean, while a Z score of 1 means the value is one standard deviation above the mean.
 How to Use Z Score Chart Normal Distribution
How to Use Z Score Chart Normal Distribution
One of the most practical applications of Z Score Chart Normal Distribution is in quality control. By using this tool, you can determine if a particular product or service is within an acceptable range of quality standards. For example, a manufacturer might use Z Score Chart Normal Distribution to determine if a particular batch of products has a higher defect rate than usual.
Another application of Z Score Chart Normal Distribution is in marketing research. By analyzing customer data and using Z scores, companies can determine which marketing campaigns are most effective and make informed decisions about ad spend.
 ### Going Deeper into Z Score Chart Normal Distribution
### Going Deeper into Z Score Chart Normal Distribution
Z Score Chart Normal Distribution can be a bit overwhelming at first, but with practice, it becomes a valuable tool for decision making. When analyzing data, it’s essential to understand how Z scores relate to probability and how to calculate them. Additionally, it’s crucial to understand that a higher Z score doesn’t necessarily mean a value is better, as it depends on what you’re analyzing and the context.
Z Score Chart Normal Distribution in Finance
One of the most common applications of Z Score Chart Normal Distribution is in finance. By using Z scores, financial analysts can analyze investment returns and determine the risk and potential returns of different investments. For example, a Z score of 1 might indicate that an investment is a safe bet, while a Z score of -1 might indicate more risk.
 Question and Answer
Question and Answer
What is a Normal Distribution?
A normal distribution is a bell-shaped curve that represents a set of data. In a normal distribution, most of the values cluster around the mean, and the rest of the values taper off towards the tail ends.
What does a Z score of 0 indicate?
A Z score of 0 indicates that a value is equal to the mean.
How can Z Score Chart Normal Distribution help in marketing?
By using Z scores, companies can analyze customer data and determine which marketing campaigns are most effective and make informed decisions about ad spend.
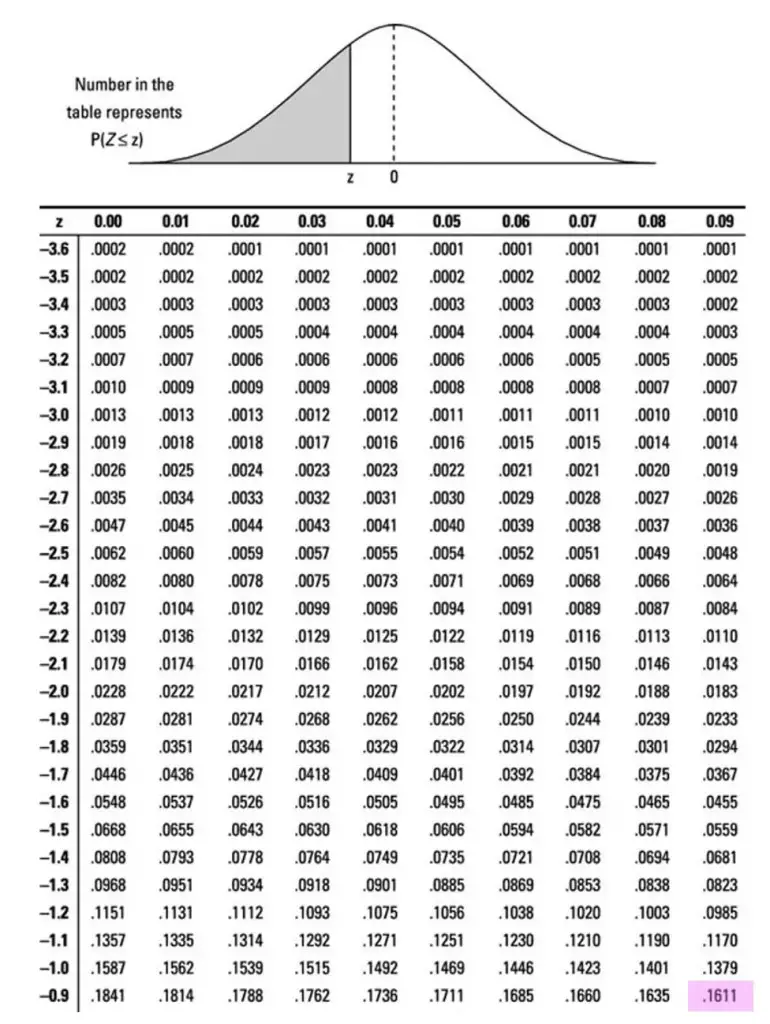
What is the formula for calculating Z scores?
The formula for calculating Z scores is simple: Z = (X - μ) / σ, where X is the value being analyzed, μ is the mean, and σ is the standard deviation.
Conclusion of Z Score Chart Normal Distribution
Understanding and using Z Score Chart Normal Distribution is a valuable skill in many fields, including finance, marketing, quality control, and more. By analyzing data using Z scores, you can make better-informed decisions and gain insights from your data. So, take the time to understand Z Score Chart Normal Distribution and related keywords such as standard deviation and normal distribution, and watch your decision-making skills improve!
Gallery
Z Score Table Normal Distribution Positive And Negative | Review Home Decor
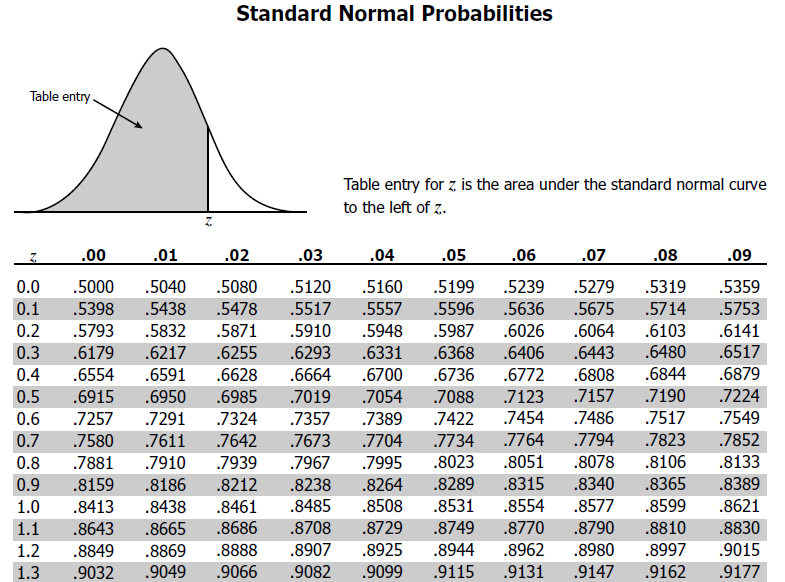
Photo Credit by: bing.com / negative statistic
Z Score Table | Standard Normal Distribution - StatCalculators.com
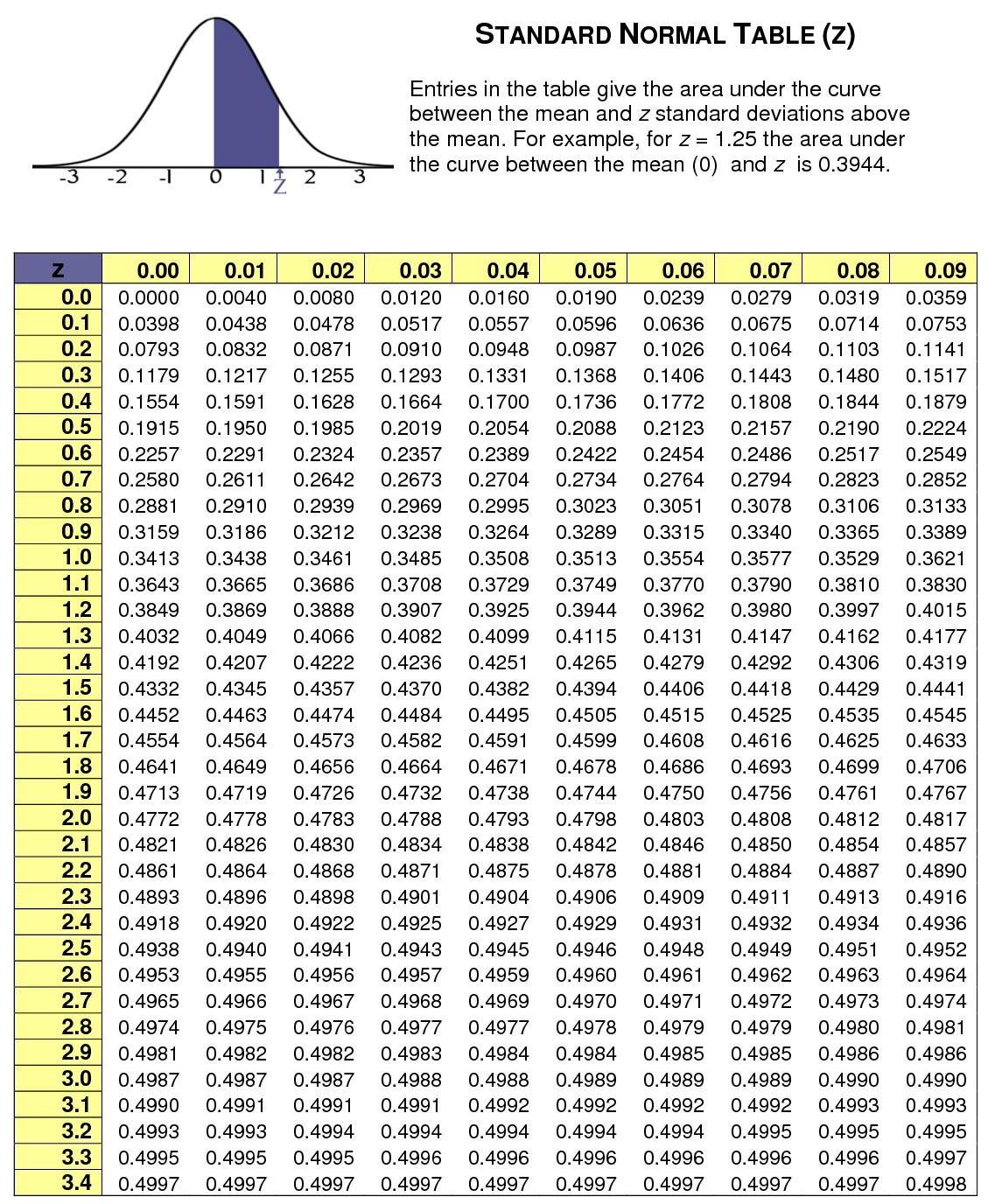
Photo Credit by: bing.com / normal score distribution table standard probability statistics calculate excel range using scores spss value deviation access tips find example variable
Z Table Normal Distribution Pdf

Photo Credit by: bing.com / stat colleges normally distributed ufl homeworklib
Normal Distribution: The Standard Normal Distribution And Using A Z
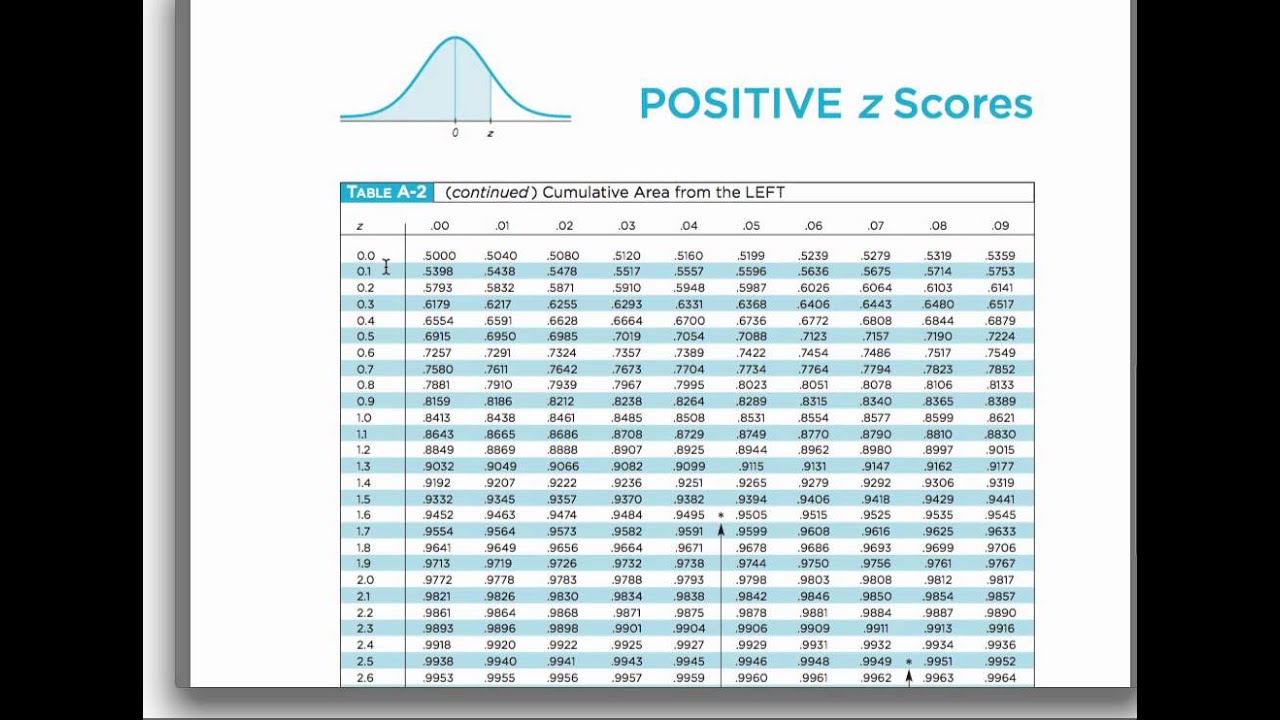
Photo Credit by: bing.com / score distribution normal chart standard
Z-Score Table For Normal Distribution | Teacher Tools | Pinterest

Photo Credit by: bing.com / normal table score distribution read math probability scores probabilities statistics calculate standard values sheet mean compute reorder point find critical