Z score conversion table
Table of Contents
Table of Contents
A Standard Score to Standard Deviation Chart is an essential tool in statistics. It is a conversion table used to change z-scores to standard deviations. If you’re planning to work in the field of statistics, then having a solid understanding of this chart is an absolute necessity!
The Pain Points:
For many students of statistics, the concept of z-scores and standard deviations can be intimidating. The idea of converting one to the other can be daunting and overwhelming, making it challenging to grasp the concepts fully. Additionally, without a solid understanding of this chart, it can be challenging to analyze data accurately and efficiently.
The Target:
The primary target of the Standard Score to Standard Deviation Chart is anyone working with statistics. This chart can be especially beneficial to people analyzing data in the fields of healthcare, sports, and other scientific disciplines.
The Main Points:
This article aimed to provide readers with an understanding of the Standard Score to Standard Deviation Chart. We covered pain points that often arise when working with this chart, such as the complexity of z-scores and standard deviations. We also went in-depth about the target audience of this chart, which is anyone in a field where data analysis is crucial. We examined the primary purpose of this chart and how it is a fundamental tool in statistical analysis.
The Purpose of the Chart:
The Standard Score to Standard Deviation Chart converts z-scores to standard deviations. A z-score is a measure of how many standard deviations a particular data point is away from the mean. This chart is particularly useful in establishing the mean score and distribution of scores, given that the data is scattered in a normal distribution pattern.
When I was studying statistics, I had an interesting personal experience with the Standard Score to Standard Deviation Chart. I was tasked with analyzing the effectiveness of a new weight loss drug. I used this chart to help me understand how many standard deviations the data was away from the mean. This process gave me an accurate picture of the drug’s efficacy, which was really eye-opening. I was amazed by how useful this chart was in helping me understand the data I was analyzing.
Understanding the Chart:
The Standard Score to Standard Deviation Chart has values of z-score on the left side, indicating the number of standard deviations from the mean. The top of the chart shows a decimal point corresponding to the second digit of the z-score values. These values combine with the number in the row and column to estimate a probability. The purpose of this chart is to help you determine the probability associated with a specific z-score.
The Formula:
The formula for calculating the conversion of the Standard Score to Standard Deviation Chart is:
Standard score (z-score) = (X-μ) / σ
Where:
X = raw data value
μ = population mean
σ = standard deviation
Personal Experience:
When I worked on a project to develop a new product, I used this chart to analyze the quality of the production. The process involved analyzing the standard deviation of specific values to determine whether the production process was consistent. Once we had a good understanding of the standard deviation, we could move forward with adjustments in the production process to improve product quality.
Question and Answer:
Q: What is the primary use of the Standard Score to Standard Deviation Chart?
A: This chart is used to convert z-scores to standard deviations, providing an accurate picture of data distribution through a normal curve.
Q: Who uses the Standard Score to Standard Deviation Chart?
A: Professionals in various scientific disciplines use this chart to gain a better understanding of data distribution and analyze deviations from the standard mean.
Q: How does the Standard Score to Standard Deviation Chart help in data analysis?
A: By providing a clear picture of the number of standard deviations between various data points, this chart helps professionals develop statistical models and understand the distribution of data.
Q: What is a z-score?
A: A z-score is a measure of how many standard deviations a specific data point is away from the mean.
Conclusion of Standard Score To Standard Deviation Chart:
As you can see, the Standard Score to Standard Deviation Chart is an essential statistical tool that helps professionals analyze data accurately and efficiently. By having a solid understanding of this chart, you’ll gain a more comprehensive understanding of data distribution, be better equipped to create statistical models, and identify potential issues. In summary, this chart is a crucial tool for professionals in any field where statistical analysis is required.
Gallery
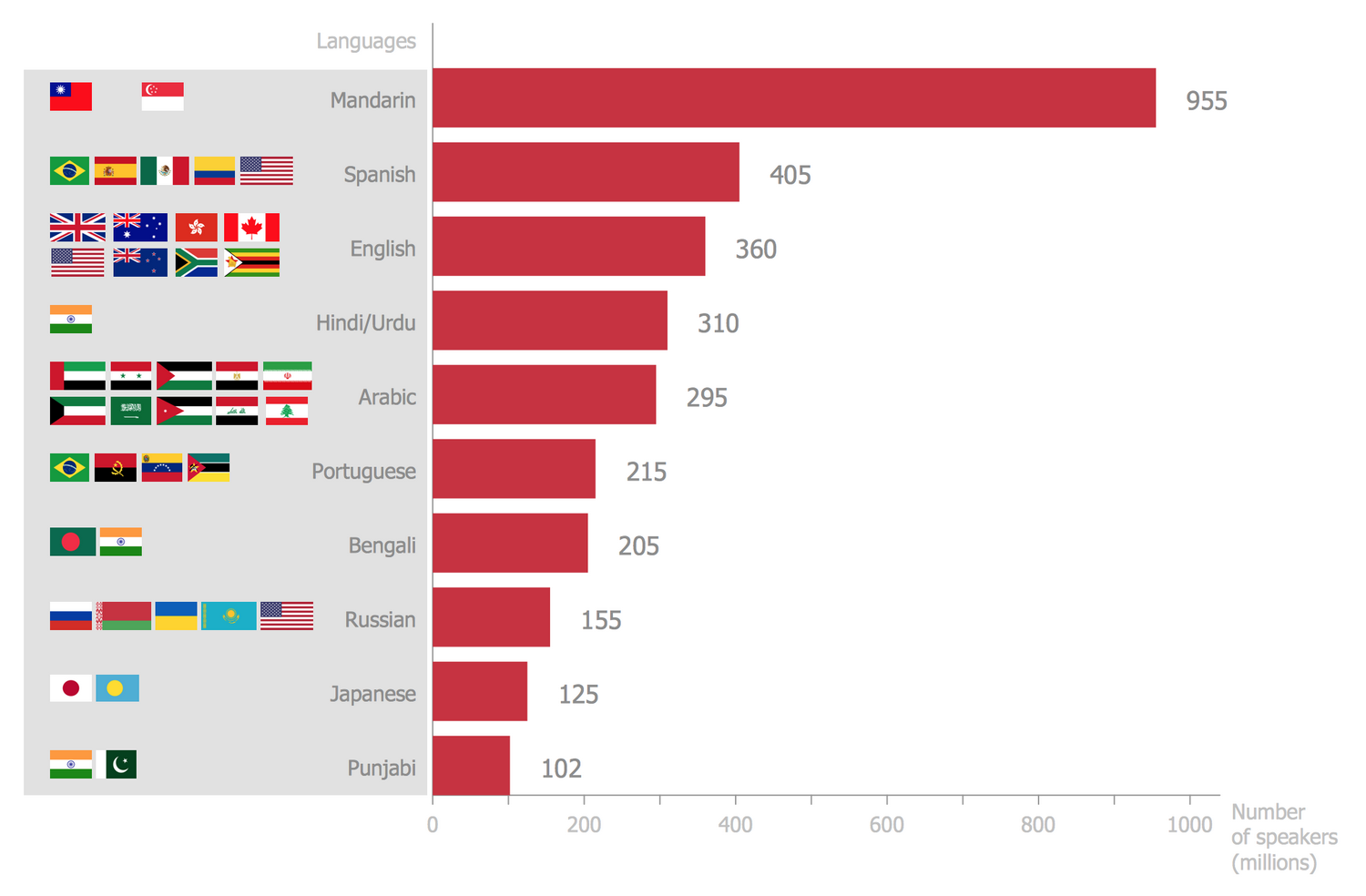
Pin On Charts

Photo Credit by: bing.com / standard score percentile conversion table scores scaled percentiles medfriendly deviation converting curve bell range use statistics charts interpretation explaining
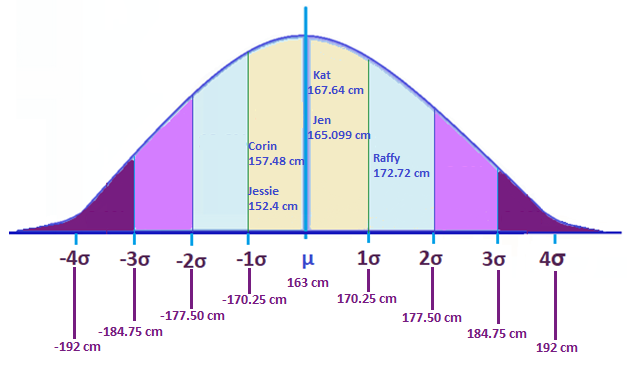
Z Score Conversion Table | School Speech Therapy, Speech Therapy

Photo Credit by: bing.com / deviations
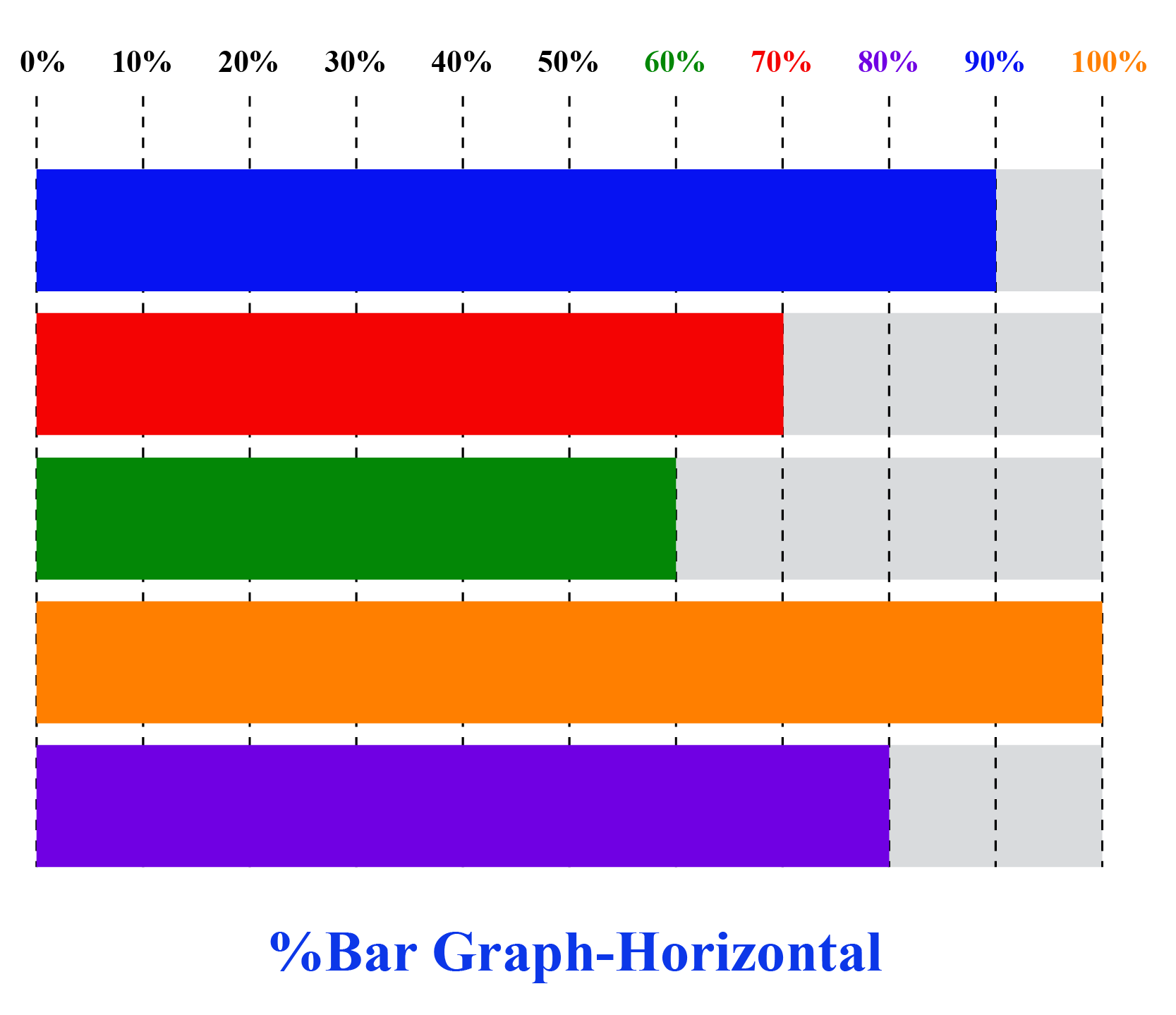
17 Best Bilder Om Bell På Pinterest | Psykologi, Charts Och Kurvor

Photo Credit by: bing.com /
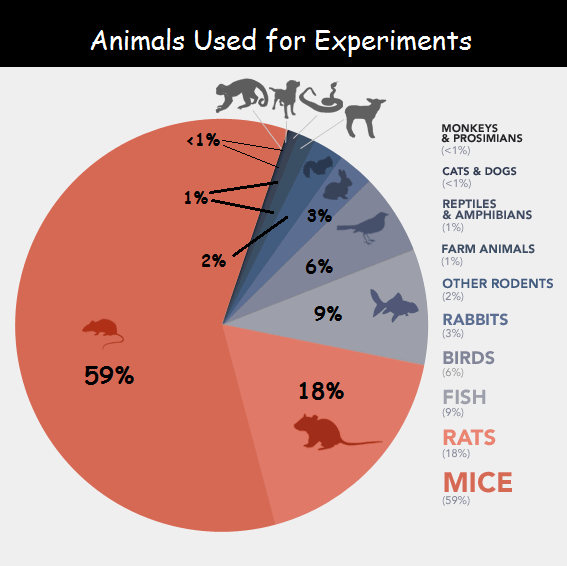
Statistics - Wikidoc

Photo Credit by: bing.com / statistics normal standard curve bell standardized graph percentile scores distribution scales testing assessment used deviations include wikidoc percentages equivalents index
Normal Curve And Standard Deviation, Z Scores, Stanines, Percentiles
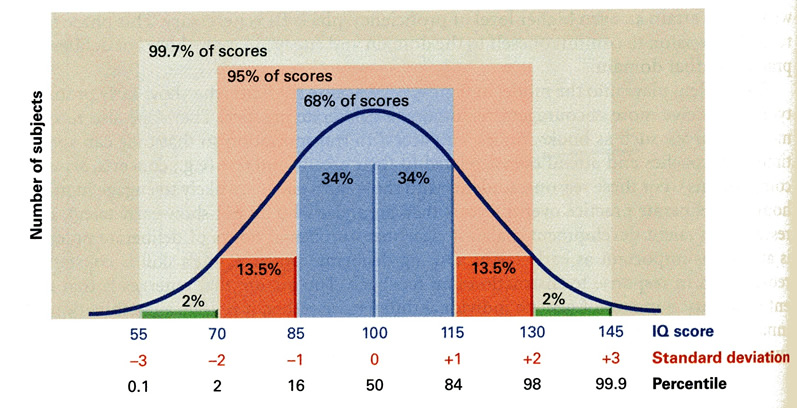
Photo Credit by: bing.com / standard deviation scores iq chart curve percentiles sat normal act statistics percentile graph bell deviations math sigma